Introduction

Control theory is a field of control engineering and applied mathematics that deals with influencing the behavior of dynamical systems. The objective is to drive a system towards a desired state by calculating and applying system inputs, while minimizing delay, overshoot, steady-state error, and ensuring stability. The aim is often to achieve a degree of optimal and robust control performance in the presence of uncertainty.

The fundamental challenge in control theory is to determine a technically feasible way to act on a system so its behavior closely matches some desired behavior, despite uncertainties in the system’s model and external disturbances. The key elements of this control problem are:

• Desired behavior The target behavior must be clearly defined as part of the control design problem. Common examples include tracking a reference trajectory, regulating around a setpoint, or optimizing some performance index.

• Feasibility The control solution must satisfy constraints on the available inputs, actuator capabilities, safety limits, etc. The controller must be realizable with available technology.

• Uncertainty Precise knowledge of the system is rarely possible. There will always be some uncertainty in the model parameters, unmodeled dynamics, disturbances, and measurements.

• Action Control action is applied through manipulated inputs that command the system actuators. The choice of manipulated inputs and pairing with actuators is a key design decision.

• Disturbances Real systems experience unknown external disturbances that affect the system behavior and must be accounted for. Rejecting disturbances is often a key control objective.

• Approximate behavior Due to uncertainty, no controller can achieve perfect setpoint tracking or disturbance rejection. There will always be some approximation error. Controllers must be designed to achieve some acceptable level of performance in spite of these challenges.

• Measurements Measuring the system outputs is essential for closing the feedback loop and allowing the controller to determine the effect of its inputs on the system behavior. Noise on measurements must also be accounted for.

In this training, we will focus on classical control methods applied to linear time-invariant (LTI) systems. We will model an inverted pendulum system, estimate its parameters, analyze stability/controllability/observability, design a state observer, and synthesize PID and LQR controllers. These tools will demonstrate how to design controllers that are robust to uncertainty and reject disturbances for stable control.

For this training we will use the Python Control Systems Library (python-control). It is a Python package that implements basic operations for analysis and design of feedback control systems.

We will use make use of helper classes and functions classes and functions that we will use throughout the rest of the notebook. The most important of which are:

• InvertedPendulumEnv

• FeedbackController

• Observer

• ConstantController

• RandomController

• ProportionalController

• SimulationResults

• simulate_environment()

Branches of Control Theory

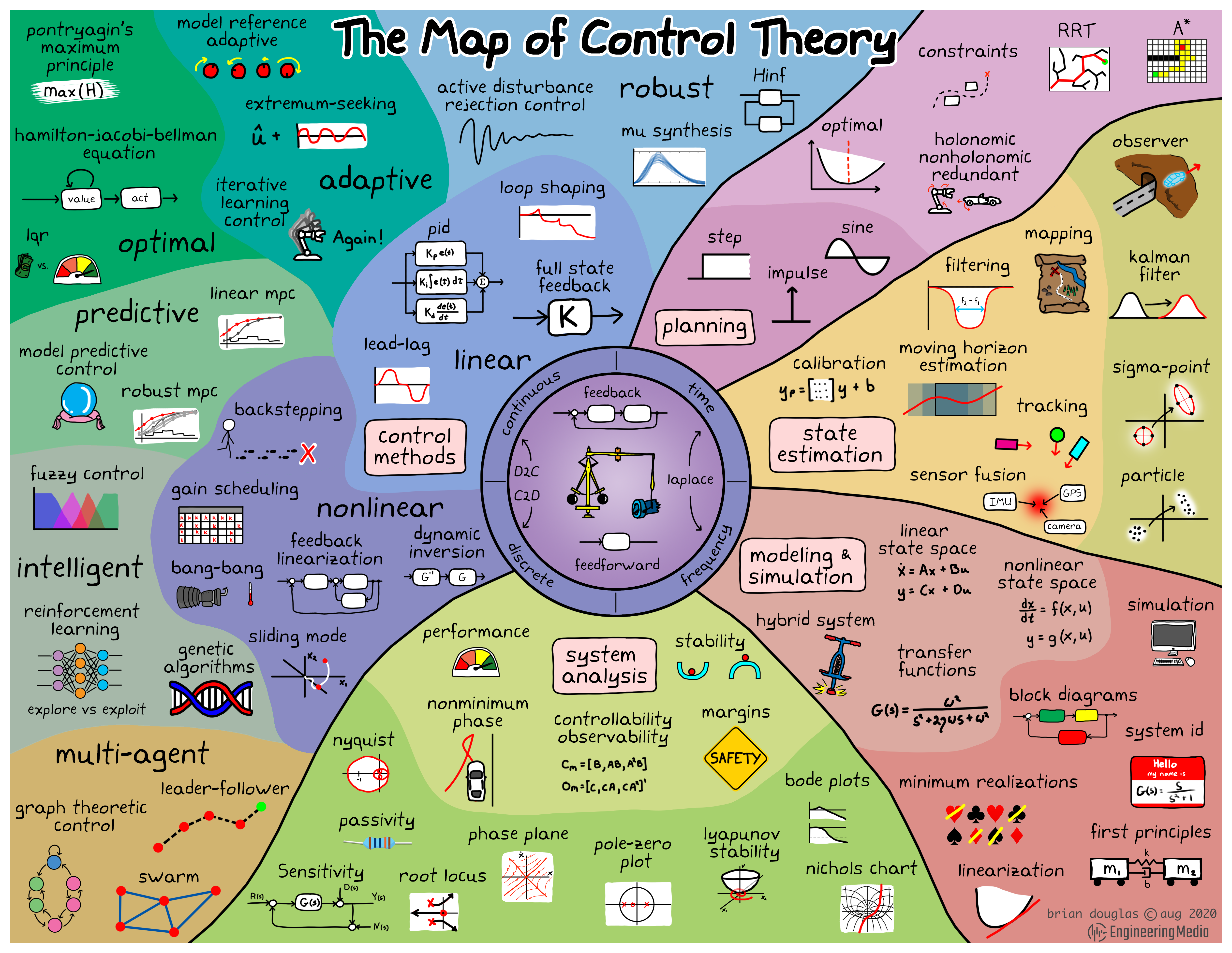
Fig. 1 The Map of Control Theory

There are different branches of Control Theory:

• Classical Control

  deals with the behavior of linear dynamical systems with inputs, and how their behavior is modified by feedback, using the Laplace transform as a basic tool to model such systems. It is limited to single-input and single-output (SISO) system design.

  The most common controllers designed using classical control theory are PID controllers.

• Modern Control

  deals with the behavior of linear or non-linear dynamical systems with inputs, and how their behavior is modified by feedback, using the state-space representation as a basic tool to model such systems. It can deal with multiple-input and multiple-output (MIMO) systems.

  Optimal, adaptive and robust control theories come under this division.

• Optimal Control

  deals with finding a control for a dynamical system over a period of time such that an objective function is optimized.

• Adaptive Control

  adapt to a controlled system with parameters which vary, or are initially uncertain.

• Robust Control

  an approach to controller design that explicitly deals with uncertainty.

Control Theory and Machine Learning

Modern machine learning and control theory share deep theoretical connections. Framing machine learning problems as dynamical systems, which we refer to as control theory for machine learning, opens up new ways to analyze neural network training and design adaptive controllers.

Conversely, we can use machine learning to help solve large and complex control problems, which we refer to as machine learning for control theory.

Control Theory for Machine Learning

Control theory provides key concepts to guide the development of machine learning algorithms.

• Viewing neural networks like deep residual networks (ResNet) as dynamical systems allows control stability and optimality principles to ensure robust training.

• Framing learning as an optimization problem enables control techniques like differential dynamic programming to improve convergence of algorithms like stochastic gradient descent.

• The need to balance exploration and exploitation in reinforcement learning is addressed by stochastic optimal control theory.

Overall, control theory provides a rigorous mathematical framework to guarantee crucial learning properties. The system dynamics perspective further allows the training process itself to be controlled for faster convergence. Bridging machine learning with concepts from control is leading to new theories and training methods with stability and optimality guarantees.

Machine Learning for Control Theory

Modern machine learning provides useful tools and perspectives for control theory. Framing control problems as data modeling tasks enables powerful function approximation, estimation, and optimization techniques from machine learning to be applied. For example:

• Neural networks can learn to approximate complex dynamics for model predictive control (MPC).

• Reinforcement learning explores optimal policies like dynamic programming to control complex robots.

• Kernel methods enable non-parametric system identification without relying on predefined model structures.

• The Koopman operator is a data-driven tool to infer properties and facilitate control of unknown nonlinear systems.

Beyond specific techniques, a machine learning viewpoint focuses on what can be learned from data about a control system’s unknown dynamics. This data-driven approach is key for adaptive and nonlinear control of complex systems.

If you want to learn to learn more about this specific topic, consider attending our Machine Learning Control training.

Control Theory and Reinforcement Learning

The predominant sub-field of Machine Learning is Supervised Learning. Its goal is make the output of the model mimic the labels y given in the training set. In that setting, the labels gave an unambiguous right answer for each of the inputs.

In Reinforcement Learning (RL), we do not have labels for the inputs and instead have to rely on a reward function, which indicates to the learning agent (i.e. model) when it is doing well, and when it is doing poorly.

RL studies how to use past data (experience) to enhance (learning) the future manipulation of a system, which is precisely the scope of Control Theory. Despite that, the two communities have remained disjointed and that has led to the co-development of vastly different approaches to the same problems.

The main differences between the two lie in how the system is modeled and the approaches taken to design controllers/agents:

• In Control Theory, we explicitly model the system using knowledge about the equations governing its behaviour, by estimating the parameters of such equations or by fitting a model on measurements from the system.

• Whereas in RL, we do not generally model the system and instead learn directly the agent that maximizes the expected reward while interacting with the environment.

Fig. 2 Feedback Control in Control Engineering

Fig. 3 Feedback Control in Reinforcement Learning

Terminology

Here are a list of terms commonly used in Reinforcement Learning, and their control counterparts:

1. Environment = System
2. Agent (Policy) = Controller or Regulator
3. Action = Decision or Control
4. Observation = Measurement
5. Reward = (Opposite of) Cost

If you want to learn about reinforcement learning, consider attending our Safe and efficient deep reinforcement learning training.

System

Inverted Pendulum

Fig. 4 Balancing cart, a simple robotics system circa 1976 - Wikipedia.

An inverted pendulum is a pendulum that has its center of mass above its pivot point. It is unstable and without additional help will fall over.

The inverted pendulum is a classic problem in dynamics and control theory and is used as a benchmark for testing control strategies. It is often implemented with the pivot point mounted on a cart that can move horizontally under control of an electronic servo system as shown in the image.

For the simulation we will use a modified version of the CartPole environment from gymnasium.

It has the following possible action and observations:

Num	Action	Control Min	Control Max
0	Force applied on the cart	-10	10

Num	Observation	Min	Max
0	position of the cart along the linear surface	-3.0	3.0
1	linear velocity of the cart	-Inf	Inf
2	vertical angle of the pole on the cart	-24	24
3	angular velocity of the pole on the cart	-Inf	Inf

error: XDG_RUNTIME_DIR not set in the environment.

Exercise 1

• What can we say about the system? Is it stable?

• How can we balance the pendulum?

Naive Control

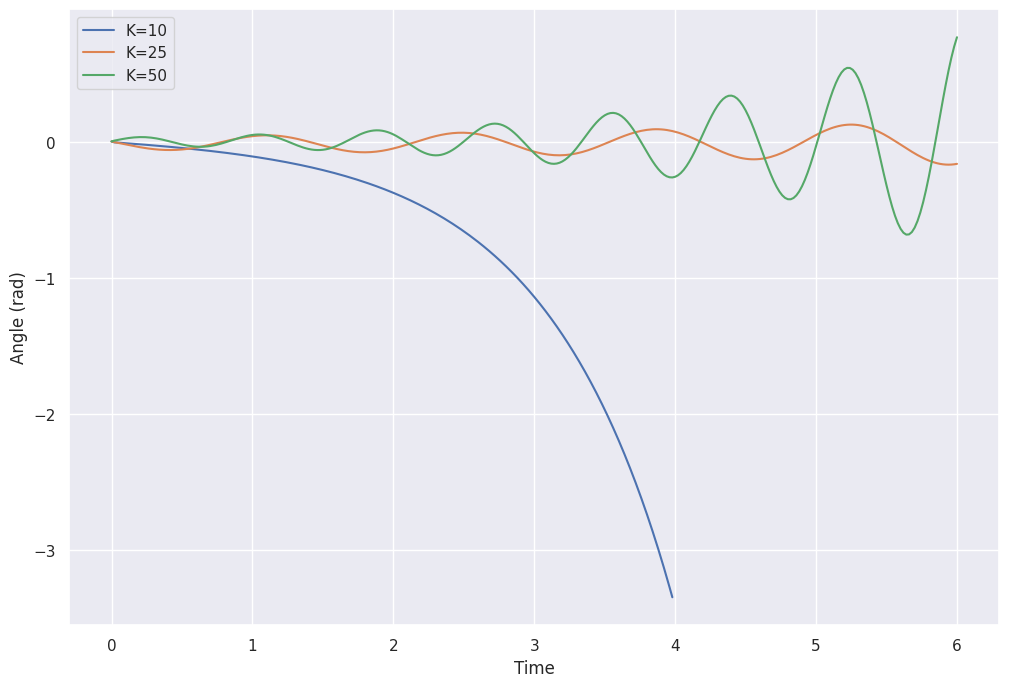
If we try to balance an elongated object on our hand, we intuitively try to move our hand in the same direction in which the object is falling. We can use this intuition to make a very simple and straightforward controller.

\[ u(t) = K * \theta(t) \]

with \(K \gt 0\)

In order to test this idea we implement the ProportionalController class and use it with our environment with different values of the gain K.

error: XDG_RUNTIME_DIR not set in the environment.

K = 10

K = 25

K = 50

Let’s plot the trajectories for these values of \(K\).

error: XDG_RUNTIME_DIR not set in the environment.

Control Systems Classification

There are two types of control loops:

• Open-loop control (feedforward)

  An open-loop control system operates without feedback, which means that the output is not measured or compared to the desired input. They are simple and inexpensive to implement. They are often used in systems where the output does not need to be precisely controlled. For example, a washing machine may use an open-loop control system to regulate the water level.

• Closed-loop control (feedback)

  A closed-loop control system, on the other hand, operates with feedback, meaning that the output is measured, and corrective action is taken to ensure it always matches the desired input. They are more complex and expensive to implement. However, they offer greater precision and accuracy in controlling the system’s output. Closed-loop control systems are often used in critical applications, such as aerospace engineering or medical devices

Types of Systems

• Time-Invariant (TI) or Time-Variant (TV).

• Linear or Non-Linear.

• Continuous-time or Discrete-time.

• Deterministic or Stochastic.

Controller Design

1. Problem Formulation

2. Modeling

   1. Define a mathematical model that represents the system.

   2. Determine properties of this system: Identifiability, Stability, Observability and Controllability.

   3. Determine model’s parameters, if they’re not known already.

   4. (Optional) Linearize model around operating point.

   5. (Optional) If it’s a continuous-time system and we’re using a digital controller, discretize it to obtain a discrete-time system.

3. Control Design

   • Design a controller to stabilize the system.

4. Evaluation

   1. Simulate the closed-loop system in order to validate the controller design.

   2. Use controller with actual system.